ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Любое преобразование кодов в машине основано на выполнении над ними логических операций. К логическим относятся операции над наборами двоичных (принимающих только значения 0 и 1) аргументов, в результате выполнения которых получают единственное значение: 0 или 1. Логические операции могут быть описаны с помощью специальных функций, принимающих 0 и 1 на наборах двоичных переменных и называемых булевыми функциями. Число всевозможных булевых функций от п переменных равно 2 и, следовательно, растет очень быстро с ростом п. Для двух переменных число всех булевых функций равно 16, а для одной переменной — 4. Функции одной и двух переменных играют важную роль в теории переключательных схем (схем, реализующих логические преобразования дискретных сигналов).
Таблица 3.2
| Значение
аргумента |
Значения функций
|
|||
| X | f1 | f2 | f3 | f4 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
Множество всех булевых функций от и переменных может быть описано конечной таблицей, число строк которой равно 2", а число столбцов — 22 . Например, все четыре булевы функции от одной переменной могут быть описаны табл. 3.2.
Первые две функции не требуют для своей реализации специальных аппаратурных затрат, так как первая f1 (носящая название "константа 0") соответствует разрыву цепи передачи сигнала, а вторая f2 ("константа 1") — постоянному соединению. Третья функция f3 носит название "функции повторения" (имеется в виду повторение значения аргумента), а последняя f4 — "функции отрицания", или "функции инверсии".
В электрических цепях элемент, называемый буфером и служащий для развязки цепей и согласования нагрузок, может реализовывать функцию f3, а так называемый инвертирующий буфер — функцию инверсии f4. Функцию f3 могут выполнить два последовательно включенных инвертора, т. е. элементы, реализующие функцию инверсии сигнала f4.
Это свойство инвертора использовано в схеме буфера шины адреса ПМ-ЭВМ (см. §6.3).
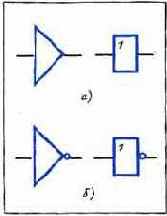
Рис. 3.1. Схемные обозначения буфера (а) и инвертора (б)
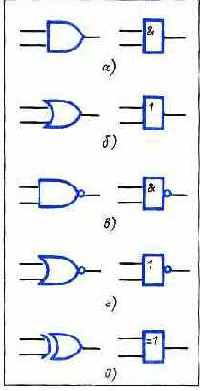
Рис. 3.2. Схемные обозначения:
а — элемента И; б — элемента ИЛИ; в - элемента И-НЕ; г -элемента И ЛИ-НЕ; д — элемента ИСКЛЮЧАЮЩЕЕ ИЛИ
Схемное обозначение буфера приведено на рис. 3.1,а, а инвертора — на рис. 3.1,6. Инвертор является весьма распространенным элементом логических схем, поскольку входит в состав других логических элементов, реализующих более сложные булевы функции. На схеме рис. 3.1 приведены по два схемных обозначения буфера и инвертора. Первое обозначение используется в основном в англоязычной литературе, второе — в отечественной и рекомендовано ГОСТ.
Среди всех 16 возможных булевых функций от двух переменных наибольшее распространение получили следующие пять функций, описываемые в табл. 3.3.
Функция f5 носит название функции логического умножения (конъюнкции), или функции И. Она реализуется с помощью логического элемента, называемого схемой И. Графическое обозначение этого элемента приведено на рис. 3.2,а. К особенностям работы элемента И относится то, что сигнал на его выходе, соответствующий логической единице, появляется только в том случае, если аналогичные сигналы присутствуют одновременно на его двух входах. Если же хотя бы на одном входе элемента И сигнал нулевой, выход также принимает значение 0. Понятие функции (схемы) И естественным образом расширяется на п переменных (входов).
Функция f6 носит название функции логического сложения (дизъюнкции), или функции ИЛИ. Она реализуется с помощью логического элемента, называемого схемой ИЛИ. Графическое обозначение элемента ИЛИ приведено на рис. 3.2,6. В отличие от схемы И на выходе элемента ИЛИ единичный сигнал появляется при наличии аналогичного сигнала на любом входе. И только если на обоих входах элемента ИЛИ присутствуют нулевые сигналы, на его выходе формируется тоже нулевой сигнал.Аналогичным образом вводится понятие и-входового элемента ИЛИ.