ОПЕРАЦИИ
Рассмотренные в предыдущем параграфе логические операции и описываемые ниже арифметические операции реализуются в арифметическо-логическом устройстве (АЛУ) микропроцессора, на котором построена ПМ-ЭВМ. Операции выполняются над 8-разрядными двоичными числами, причем старший (левый) разряд может использоваться для представления знака числа (значение 0 указывает на положительное число, а 1 — на отрицательное).
Сложение двоичных чисел производится по тем же правилам, что и сложение десятичных чисел, за исключением того, что перенос в следующий разряд осуществляется при сумме в данном разряде, равной 2, а не 10. Пусть, например, требуется сложить два числа:
00011 010B = 26D
+ 00001 100 В = 12D
00 100 110B=38D.
При сложении крайних правых четырех разрядов имели место все четыре возможные комбинации сложения одноразрядных чисел: 0+0=0, 1 + 0 = 1, 0+1 = 1, 1+1=0. В четвертом разряде сумма равна 2D, или 10 В. Следовательно, необходим перенос единицы из четвертого разряда в пятый. Тогда в пятом разряде опять же 1 + 1 = 0 и после переноса единицы в шестой разряд сумма в шестом разряде будет 1 + 0+0=1.
Нетрудно заметить, что реализация этих операций может быть выполнена с помощью всего двух логических элементов: суммы по модулю 2, или ИСКЛЮЧАЮЩЕГО ИЛИ, реализующего функцию f9, соответствующую выходу суммы S, и элемента И, реализующего функцию f5, соответствующую выходу переноса в следующий разряд С (рис. 3.3,с). Эта схема сложения одноразрядных чисел без учета входного переноса из предыдущего разряда называется полусумматором.
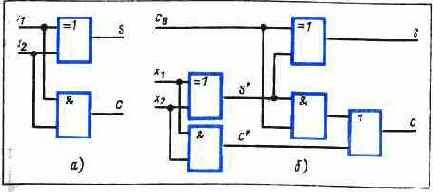
Рис. 3.3. Одноразрядные суммирующие схемы: а - полусумматор; б - полный сумматор
Чтобы реализовать сложение с учетом переноса из предыдущего разряда, необходимо использовать два полусумматора, соединив их так, как показано на рис. 3.3,6. Эта схема носит название полного сумматора, или одноразрядного сумматора. Для сложения двух 8-разрядных двоичных чисел потребуется 8 одноразрядных сумматоров, соединенных таким образом, чтобы сигнал переноса передавался в каждый следующий разряд на вход Св соответствующего полного сумматора.
Сигнал переноса из самого старшего разряда запоминается в специальном триггере, называемом триггером флага переноса, для указания переполнения, имевшего место при сложении.
Поскольку, как указывалось выше, старший разряд может отводиться под знак числа, с помощью 8-разрядной суммирующей схемы можно оперировать как с любыми целыми положительными числами в диапазоне от 00 000 000 В = OD до 11 111 111 В = 25 5 D, так и с целыми положительными и отрицательными числами в диапазоне от 01 111 111 В = 127D до 10 000 000 В = -128D (в этом случае единица в старшем разряде указывает на отрицательное число, а нуль - на положительное).
Для вычитания одного числа из другого используется специальное кодовое представление отрицательных чисел, называемое дополнительным кодом. Дополнительный код (иначе, дополнение до 2) получается прибавлением единицы к младшему разряду инверсного, или обратного, кода числа (дополнения До 1). Сложение уменьшаемого с вычитаемым, представленным в дополнительном коде, приводит к результату, который получился бы при обычном вычитании. Таким образом, не нужно строить специальную схему для операции вычитания, а можно
воспользоваться все той же схемой 8-разрядного сумматора. Пусть, например, требуется выполнить вычитание: 38 D — 26 D. Перейдем к дополнительному коду для числа — 26. Инвертируя код числа 26D и прибавляя единицу в младшем разряде, получаем:
00 011 010 — прямой код 11 100 101 — обратный код
+
1
11 100 110 — дополнительный код. Теперь выполним сложение:
00100 110В + 11 100 110В
100001 100 В =12D.
В результате получили двоичный код десятичного числа 12 D и перенос из старшего разряда. Этот сигнал может быть использован при выполнении арифметических операций с 16-разрядными числами по частям в одном 8-разрядном сумматоре. При этом сначала производится сложение в дополнительном коде младших разрядов суммируемых чисел и запоминание сигнала (единицы) переноса, а затем сложение старших разрядов с учетом этого сигнала переноса.
Для выполнения операций умножения и деления специальных команд в микропроцессоре КР580ИК80А не предусмотрено. Поэтому эти операции в ПМ-ЭВМ выполняются программным путем с использованием операций сложения, сложения с дополнительным кодом числа (вычитания) и сдвига (см. § 9.1).
Арифметические операции можно производить также над десятичными числами, закодированными так называемыми двоично-десятичными кодами (двоично-кодированное представление десятичного числа). При таком представлении чисел каждая десятичная цифра кодируется четырехразрядным двоичным кодом (кодом прямого замещения, или кодом 8421). После сложения двух двоично-кодированных чисел для получения правильного результата необходимо выполнить коррекцию результата этой операции. Для этого используется блок десятичной коррекции. Он осуществляет требуемую коррекцию результата путем исполнения специальной команды "десятичной коррекции" DAA (см. список команд в приложении 1), которую необходимо выполнить после команды сложения.