При решении задачи на различных
При решении задачи на различных уровнях сложности под МП могут пониматься различные конструктивно-функциональные модули. Если речь идет о реализации МПУ на базе МПК, то в данном случае под МП понимаются БИС АУ, процессорные секции и т. п. Если определяется оптимальный состав микропроцессорной системы управления ЛА или сложным радиоэлектронным комплексом, то в качестве МП (используются либо отдельные микро-ЭВМ, либо функциональные модули типа рассмотренных в § 1.2. Для одних задач МП могут конструктивно представлять собой БГИС, для других — функциональную ячейку. Кроме МП, которые программно реализуют функции, в список элементной базы включены также модули, реализующие некоторые функции аппаратным или программно-аппаратным способом. Число типов таких модулей (как и МП) очень велико: БИС умножителей, сумматоров, арифметических расширителей (арифметика с плавающей запятой); модули, реализующие сложные операции, например МП БО БПФ (см. рис. 2.3), и др.
При задании исходной совокупности МП необходимо определить множество М процессорных модулей, некоторая комбинация которых (МосМ) является оптимальным вариантом построения обрабатывающей части МПУ. Для определения Мо надо исходить из особенностей конкретного применения МПУ в составе РЭУ: условия эксплуатации, энергетические ресурсы, конструктивная совместимость с РЭУ и др. Кроме того, необходимо учитывать следующие характеристики МП:
программные возможности: разрядность; набор команд; методы адресации; время выполнения команд; число РОН, доступных пользователю; наличие стека и его характеристики; максимальная адресуемая память;
аппаратные возможности: максимальная рабочая частота синхронизации, напряжение питания, возможность совмещения с другими логическими схемами, потребляемая мощность, сложность схемы МП, наличие в его составе вспомогательных элементов для расширения функциональных возможностей; возможность комплектация вспомогательными элементами, например, аппаратные умножители, интерфейсные схемы, арифметика с плавающей запятой и др.; размеры корпуса « число выводов, число портов ввода-вывода и др.;
системные характеристики: наличие прерываний, включая их уровень, число и систему приоритетов; ПДП; наличие программного обеспечения (редактор, отладчик, ассемблер, вспомогательное ПО для записи программ в ППЗУ, пакет тригонометрических функций, диагностические программы для МП и памяти) и т. п.;
наличие документации: описания МП, руководящего технического материала по применению, вспомогательной информации;
экономические возможности: стоимость МП, наличие опыта работы с данным МП, .наличие основного и резервного поставщика и т. п.
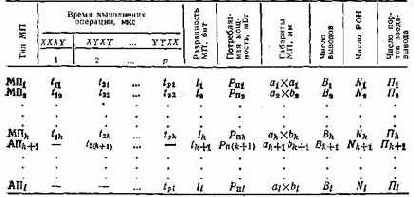
Совокупность заданных МП М представляет собой открытое множество, которое расширяется при появлении новых МП, отвечающих перечисленным выше требованиям. Каждый МП представляет собой строку таблицы, которая характеризуется рядом элементов (параметров МП). В табл. 3.4 приведен минимальный перечень параметров. При решении конкретных задач число рассматриваемых параметров может быть увеличено.
Важнейшей характеристикой МП является набор команд и время их выполнения. Микропроцессоры, входящие в М, имеют различные системы команд. Независимость модели программы от системы команд конкретных МП достигается выбором языка моделирования.
Проектирование специализированных МПУ, ориентированных на решение задач определенного класса, обычно требует разработки своего языка моделирования. Уровень разработки этого языка может быть различным и зависит от того, какие задачи ставятся разработчиком на данном этапе проектирования.
В общем случае в качестве языка моделирования могут быть использованы алгоритмические языки, ассемблеры, системы команд специализированных вычислительных устройств, решающих подобные задачи, и т. п. В простейшем случае язык моделирования может быть получен путем анализа алгоритмов обработки и систем команд исходных МП. Упрощенный вариант анализа может представлять собой такую последовательность действий:
1. Из исходного множества различных систем команд (МК) выбирается MKi=MK, наиболее соответствующая реализуемому алгоритму (наличие операций умножения, деления, ПДП и др.).
2. MKi дополняется операторами, наиболее часто встречающимися при реализации алгоритмов данного класса (тригонометрические преобразования, комплексное умножение и т. п.). Кроме того, МКг может дополняться операторами, реализуемыми ап-паратно.
3. Система команд каждого МП расширяется путем включения в ее состав подпрограмм реализации дополнительных операторов.
Сформированная, таким образом, система команд по типу выполняемых операций имеет аналоги в системе команд любого МП. Это делает графовую модель программы, представленную в такой системе команд, независимой от типа МП. Особенности систем команд конкретных МП учитываются значением аргумента вершины модели t{j, так как в одном случае это команда и значение ta меньше, в другом — подпрограмма и значение tij соответственно больше. В отличие от МП АЛ реализует одну или несколько операторов выбранного языка моделирования. Кроме набора команд каждый МП характеризуется конструктивными параметрами: разрядностью l, потребляемой мощностью Рп, габаритами, числом выводов. Перечень этих параметров может быть расширен.
Графовая модель программы с учетом принятых в § 3.2 гипотез представляет собой цепь Маркова. Поэтому среднее значение и дисперсия времени ее выполнения определяются следующим образом [46]:
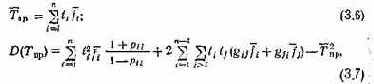
где fi — среднее значение частоты повторения i-го шага программы при однократном проходе; gij — вероятность попадания в состояние Xj, если хi является начальным состоянием: ри — вероятность перехода из вершины Xi в Xj.
Итак, исходя из (3.4), задачу выбора числа и типа МП на I этапе конструкторского синтеза МПУ можно свести к определению группы МП Мо=М, обеспечивающих решение алгоритма при выполнении ограничений Tпр<T, б<бдоп.
Решение задачи включает несколько стадий. Вначале определяются МП, обеспечивающие решение задачи в однопроцессорном варианте. Для тех МП, быстродействие которых недостаточно для однопроцессорного варианта решения задачи, анализируется возможность повышения их производительности путем подключения аппаратных процессоров либо распараллеливанием вычислений.
При расчете погрешности вычислений МПУ исходят из гипотезы о независимости ошибок округления в цепочке последовательных элементарных операций [47]. Среднее квадратическое значение погрешности вычислений МПУ
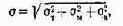
где ат, стм, аи — средние квадратические значения трансформируемой, методической и инструментальной погрешностей соответственно.
Трансформируемые ошибки порождаются ошибками задания исходных величин. Эти ошибки в процессе выполнения арифметических операций изменяют свою величину (трансформируются). Значение ат можно определить из выражения
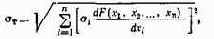
где F(xi, X2, ..., хп) — вид реализуемой функции; бi — среднее квадратическое значение погрешности аргумента Xi. Значение погрешности представления входных данных
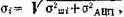
Методические погрешности представляют собой погрешности численных методов, принятых для вычисления функции F(xu х2, ..., хп). Поскольку алгоритм обработки задан, то, следовательно, ам определено.
Инструментальные погрешности обусловлены конечным числом разрядов, предназначенных для представления операндов и необходимостью округления результатов некоторых элементарных арифметических операций. Результирующая инструментальная погрешность представляет сумму накопившихся ошибок при последовательных округлениях элементарных операций. Величина ее определяется реализуемым алгоритмом и разрядностью МП. Результирующее значение инструментальной погрешности
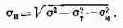
Проведя предварительные вычисления, алгоритм выбора типа и числа МП можно представить в виде следующей последовательности действий:
1. Определяется разрядность ячеек ОЗУ, предназначенных для хранения входного массива данных: lBX = ]log2 UМакс/бвх[, где Umskc — амплитуда входного сигнала; бвх — средняя квадратиче-ская погрешность входного сигнала.
2. Определяется число Дl:
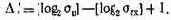
3. Определяется число разрядов, требуемое для компенсации инструментальной погрешности:
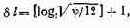
где ф — длина цепочки последовательных операций с округлениями.
4. Определяется разрядность МП, обеспечивающая при данной би погрешность представления результатов вычислений не выше бдоп.
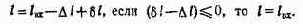
Методика расчета разрядности МП, работающих в системах счисления с плавающей запятой, рассмотрена в [48].
5. Корректируется время выполнения операций, представлен-ных в табл. 3.3 с учетом разрядности МП l и времени распространения сигналов переноса.
6. С учетом элементарных преобразований графов, представленных на рис. 3.4, упрощается исходная модель программы.
7. Частота повторения начальной вершины f1 принимается равной 1. Последовательно двигаясь от вершины к вершине, определяются средние частоты их повторения:

где fi — средние частоты повторения предыдущей вершины; т — число дуг, входящих в вершину Xj.
8. На основании данных табл. 3.3 (ti) и результатов, полученных в предыдущем пункте, из выражения (3.6) определяется среднее время выполнения программы каждым МП, представленным в табл. 3.3.
9. С помощью выражения (3.7) определяется D(Tnp). Для упрощения программирования выражения (3.7) оно может быть представлено ib следующем виде [46]:
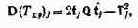
где ij={ti}j — вектор-столбец значений выполнения шагов программы j-м МП; ij — -{tjifi}; Q=||qij|| — матрица, элементы которой определяются следующим образом:
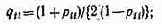
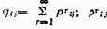
— вероятность попадания на r-м шаге выполнения программы в состояние Xj, если Xi является начальным состоянием.
Значения элементов матрицы Q определяются значениями матрицы вероятности переходов ||рц||.
10. Для определения верхней границы 7ПР необходимо знать закон распределения плотности вероятности значений ГПР. Если этот закон неизвестен, то можно использовать неравенство Чебы-шева, дающее оценку вероятности того, что абсолютное отклонение случайной величины от ее среднего значения |Tпр — Tпр| не превзойдет некоторого положительного числа a с вероятностью р:
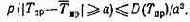
11. Полученное значение 7щ, сравнивается с Т. Микропроцессоры, имеющие значение Тпр<T, образуют группу M0.
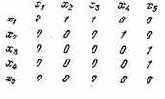
Рис. 3.5. Матрица данных
12. Для определения возможности повышения производительности МП необходимо оценить степень параллелизма решаемого алгоритма. Две операции могут выполняться одновременно (параллельно) разными МП, если их операнды определены. Подпрограммы с независимыми данными могут быть определены на основании анализа матрицы данных O = ||ojj||, причем

Матрица О имеет размерность пхп. Строки матрицы совпадают с вершинами графа G(X, U), а столбцы представляют собой вершины-последователи. Иными словами, элементы столбца указывают вершины, результаты операции которых являются операндами данной вершины.
На рис. 3.5 приведен пример матрицы данных. Из анализа матрицы видно, что вершины х2 и х3 определяются только результатом операции вершины х1, следовательно, они могут быть выполнены одновременно.
Построение «матрицы О осуществляется по данным табл. 3.3. Анализируются столбцы матрицы О. Определяются столбцы с совпадающими элементами. Эти столбцы представляют собой начальные вершины подпрограмм, которые могут выполняться одновременно. Подпрограмма включает только те вершины, которые были определены на предыдущих шагах вычислений.
13. С помощью выражений (3.10) и (3.11) определяются Tпр ij, D(Tпpij), где i, j — номер подпрограммы и шип МП соответственно.
14. Сравниваются полученные значения Тпрц с Т. Если Тпр ij<. <T, то переход к п.15, если нет, то к п.16.
15. Определяется минимальное число МП (Кмп), объединенных параллельно и обеспечивающих ТПр ij<Т.
16. Оценивается число последовательно включенных МП:
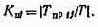
17. После анализа результатов, полученных в пп.15 и 16, оп ределяется число МП данного типа, необходимое для реализации алгоритма в реальном времени. Эти данные заносятся в массив Мо-
18. Определяется возможность реализации подпрограмм ап-г паратными процессорами (АП). Изменяются веса соответствующих вершин и корректируется значение Тпр. Если Тпр<.Т, то соответствующие МП и АП фиксируются в массиве Мо-
19. Каждый элемент массива Мо представляет собой один из возможных структурных вариантов реализации исходного алгоритма А на заданном наборе МП (см. табл. 3.4) в рамках заданных ограничений (б<7ДОп, Т<Тпр). Лучшим из вариантов будет тот, который размещается на меньшей площади монтажной платы.
Таким образом, данный алгоритм позволяет определить массив Мо, который включает тип и число МП этого типа, обеспечивающее решение алгоритма А в реальном масштабе времени аппаратным или программно-аппаратным путем с использованием одно- или многопроцессорной структуры построения МПУ.
Пример 3.1. Определить тип и число МП БИС, обеспечивающих выполнение БО алгоритма БПФ с прореживанием по времени при следующих ограничениях: Г=2 мкс; система счисления — с фиксированной запятой; аш=2 мВ: динамический диапазон входного сигнала d=45 дБ; тип монтажной платы — односторонняя печатная плата; размерность входного массива vV= 128; потери на выполнение БО — не более 4 дБ; рдоп = 0,1 Вт/см2.
Алгоритм БО БПФ с основанием г = 2 и прореживанием по времени рассматривался в § 2.1. Структурная схема алгоритма представлена на рис. 3.6,а [2]. Алгоритм реализуется на базе МПК БИС, представленных в табл. 1.2. Исключение составляет МПК БИС серии К588. Поскольку алгоритм БО включает операцию умножения, которая не может быть реализована на умножителе К.588ВР2 быстрее 2 мкс, что не удовлетворяет временным ограничениям.
Для упрощения задачи в исходный массив МП М (табл. 3.5) включены только АУ, расширители арифметических операций и схемы обмена информацией.
Содержание табл. 3.5 соответствует табл. 3.4. Состав операторов определен из анализа алгоритма БО БПФ. При оценке времени выполнения операции были сделаны следующие допущения: операции сложения (СЛ), вычитания (ВЧТ), пересылки между регистрами общего назначения (Рг — Рг) выполняются за один такт работы МП; операции пересылки память — регистр (П — Рг) » регистр — память (Рг — П) выполняются за три такта работы МП. Операция умножения последовательным умножителем КР1802ВР2 выполняется за 2 мкс, параллельными умножителями — за один такт работы МП.
Операция умножения двух 16-разрядных чисел МП К1800ВС1 и КМ1804ВС2 выполняется программно, в первом случае за 20 тактов, во втором — за 17 тактов [5]. Действительные значения параметров некоторых БИС могут незначительно отличаться от приведенных в табл. 3.5.
Первым шагом алгоритма выбора типа и числа МП является определение разрядности МП, обеспечивающей требуемую точность вычислений. Выше приведена методика определения разрядности МП для системы счисления с фиксированной запятой. Эта методика справедлива для любых цифровых вычислительных устройств. Вместе с тем, в РЭА, и в частности в цифровой обработке сигналов, вместо понятия среднее квадратическое значение погрешности на выходе устройства пользуются производным от него понятием: потери (Я), вносимые вычислителем. Под потерями понимается уменьшение отношения сигнал-шум на выходе устройства, обусловленное трансформируемой и инструментальной погрешностями. Эти погрешности называют шумами вычислений. Известно [2], что при Д<Збвх, где Д — цена младшего разряда после округления, бвх — среднее квадратическое значение погрешности на входе АУ, ошибки вычислений аддитивны с сигналом.
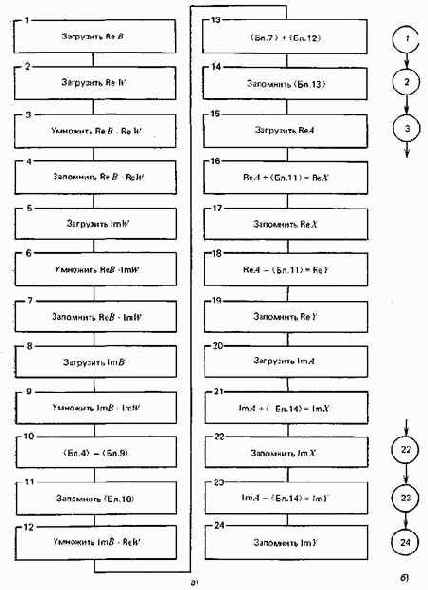
Рис. 3.6. Структурная схема алгоритма выполнения базовой операции быстрого преобразования Фурье с основанием два и прореживанием по времени (а) и ее графовая модель (б)