даны количественные оценки уровня

bсф1	bк1	Ксф=1	КК = 1	ксф=1, Кк=0,99	Ксф=1, Кк=0,95	kсф=1.	kн=0,9
UЗw/Uw ДБ	U-w/UW, ДБ	U3w/Uw, ДБ	U — w/Uw, дБ	UЗw/Uw, ДБ	U — w/Uw, ДБ	UЗw/Uw, дБ	U — w/UW, дБ
0	0		—		— 46		— 32	—	— 26
0,01	0	— 50	— 40	— 50	— 36	— 50	— 29	— 50	— 24
0,05	0	— 36	— 25	— 36	— 26	— 36	— 23	— 36	— 20
0,10	0	— 30	— 21	— 30	— 20	— 30	— 19	— З0	— 17
0,01	0,01	— 44	—	— 44	— 46	— 44	— 32	— 44	— 26
0,05	0,01	— 39	— 28	— 35	— 27	— 34	— 24	— 34	— 21
0,10	0,01	— 30	-22	— 29	— 21	— 29	— 19	— 29	— 18
0,05	0,05	— 30	—	— 30	— 47	— 30	— 32	— 30	— 26
0,10	0,05	— 27	— 27	— 27	— 26	— 26	-23	— 26	__21

В табл. 3. 1 даны количественные оценки уровня ложных сигналов для гар­монического входного сигнала Acos(w0+Q)T и различных значений Ксф, Кк, bсф1, bК1.
Отклонения разности фаз квадратурных составляющих от 90° также при­водит к появлению ложных сигналов на частоте — Q. При разности фаз ф для гармонического входного сигнала сигнал на выходе ФК можно записать в виде

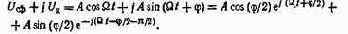
В табл. 3.2 приведены количественные оценки уровней ложных сигналов, обусловленных отклонением разности фаз каналов от 90.
Используя табл. 3.1 и 3.2, разработчик должен оценить допустимые иска­жения, определенные заданным динамическим диапазоном входного сигнала d. Если эти искажения велики, то необходимо либо предусмотреть коррекцию искажений, либо отказаться от ФК и перейти к дискретизации сигналов на не­сущей частоте w (см. § 3.4).
Алгоритм спектрального анализа включает следующие этапы:
1. Формирование подмассивов входных данных. Из массива входных от­счетов s(ri) формируется L подмассивов выходных отсчетов yi(n), где I — номер подмассива .(l=1,L). Соотношения между отсчетами подмассивов и ис­ходного массива определяет алгоритм выбора подмассивов



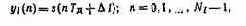
где Дl — задержка подмассива относительно начала массива; Ni — число отсче-тов подмассива. Параметры N, Ni, Тя, А1 определяются из анализа исходных данных. Число отсчетов на интервале обработки N = TmlTa, где Ти — длитель-ность интервала обработки. Значение Tи определяется требуемым расстоянием между центральными частотами соседних фильтров: rH=l/6f. Частота дискре­тизаций входного сигнала при использовании ФК Fa>ДF, число отсчетов N=ДF/бf. В данном случае N=Ni. Число подмассивов определяется соотноше­нием между длительностью интервала обработки Ти и длительностью обраба­тываемого сигнала Тс: L=TCITS. С помощью БПФ производится вычисление «скачущих» спектров на интервалах длительностью N, сдвинутых на величину скачка N3, причем Na=Al/TR. Обычно в задачах спектрального анализа N3 со­ставляет 1/4, 1/2 или 3[4N [2]. Полученные результаты анализа исходных данных определяют требования к схеме сопряжения и периферийным устрой­ствам МПУ, выполняющего спектральный анализ.
Таблица 3.2

Аф, град	0,10	0,15	0.20	0,30	0,35	0,40	0,45	0,50	0.6S	0,60	0,65	0,70	0,85	1,00
Лбл. ДБ	59,2	57,0	55,2	51,3	50,3	49,2	48,1	47,0	46,2	45.6	44.8	44,1	42,7	41,2

2. Коррекция мнимой и действительной частей входных отсчетов

Этот этап вводится в том случае, если при обработке входного сигнала с динамическим диапазоном d уровень ложных сигналов, обусловленных нели­нейностью ФК, превысит допустимый.
3. Весовая обработка входных подмассивов. Амплитудная и фазовая харак­теристики аналоговых фильтров, эквивалентных выходным отсчетам БПФ, оп­ределяются модулем и фазой весовой функции и (га):
yi(n)=si(n)v(n).
Основные параметры наиболее часто применяемых весовых функций приведены в [2]. Выбор конкретной весовой функции определяется следующими пара­метрами: уровнем боковых лепестков .До.л, крутизной ската S, полосой про­пускания фильтра Дf. Отметим, что уровень боковых лепестков с использова­нием прямоугольной весовой функции [v(n) = 1 при l<n<N] составляет — 13 дБ, S= — 6 дБ/октава.


Если требуется более высокое значение Ае.л, то необходимо вводить в алгоритм спектрального анализа этап весовой обработки.
4. Дискретное преобразование Фурье (ДПФ,)

ДПФ вычисляется по алгоритму БПФ (см. § 2.1). Существует множество алгоритмов БПФ, отличающихся друг от друга, главным образом, числом вы­полняемых операций умножения и сложения. Реализация операции умножения на МП требует значительного процессорного времени. В свою очередь, вычис­ление ДПФ составляет основную часть времени вычисления спектра входного яодмассива. Поэтому выбор наиболее эффективного (с вычислительной точки зрения) алгоритма БПФ позволит значительно улучшить конструктивные па­раметры МПУ. Анализ различных типов алгоритмов БПФ выходит за рамки данной книги. Эти вопросы изложены в [2, 42]. Хотелось бы только отметить, что количество элементарных операций, затрачиваемых на выполнение базовой операции (БО), не всегда является параметром, определяющим эффективность алгоритма в целом. Например, аппаратурная сложность МП, реализующего БО вычисления ДПФ по алгоритму числового преобразования Ферма (ЧПФ), при­мерно в 3 — 6 раз меньше сложности МП БО, реализующего БПФ по основа­нию 2. Кроме того, для решения задач обработки радиосигналов один комплек­сный отсчет для обычного БПФ содержит примерно 27 разрядов, в случае ЧПФ одно действительное слово содержит 33 разряда. Поэтому при вычислений опе­раций свертки умеренной длины (до jV=64) аппаратурный выигрыш при ис­пользовании ЧПФ-процессора получается значительным. При увеличении длины; обрабатываемого подмассива, выигрыш в аппаратурных затратах на реализа­цию БО компенсируется увеличением объема памяти [42]. Разрядность пред­ставления входных отсчетов можно оценить следующим образом: iBx»]log2 d[,. где ]а[ — ближайшее к а большее целое число. Для спектрального анализа, входных сигналов время вычисления одного выходного отсчета должно быть не­более Tд. Зная допустимое время вычисления T, а также учитывая значения lвх и N, можно ориентировочно выбрать наиболее эффективные для конкрет­ного случая алгоритмы БПФ.


Фильтрация. Частотная характеристика фильтра с бесконечной импульсной характеристикой (БИХ-фильтра) приведена на рис. 3.2. Основными исходными данными являются: частота настройки w0Тя, полоса пропускания по уровню ДА — 2Аw2Тд, полоса пропускания по уровню А — 2Дw1Tд, амплитуда пульсаций в полосе прозрачности 2AwsTд — ДВ и в полосе задержания 2AwrTa — В.
Коэффициент прямоугольности a = Дw1/Дw2. Близость коэффициента пря­моугольности а к единице определяется порядком фильтра. Поэтому задача за­ключается в выборе минимального порядка фильтра, при котором обеспечива­ются перечисленные выше параметры. Если использовать при синтезе цифро­вых фильтров в качестве аналоговых фильтров-прототипов фильтры Баттер-ворта, Чебышева или эллиптические, то для заданных параметров можно рас­считать зависимость порядка аналоговых фильтров от коэффициента прямо­угольности, а затем пересчитать эту зависимость для цифровых фильтров. На рис. 3.3 показана зависимость порядка фильтра от коэффициента прямоуголь­ности аналоговых фильтров и цифровых фильтров, причем b = = tg aДw2Tд/tg Дw2Tд.

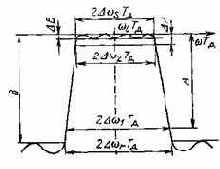
Рис. 3.2. Частотная характеристика ци­фрового БИХ-фильтра

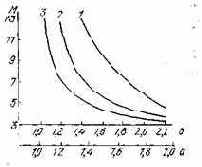
Рис. 3.3. Зависимость порядка фильтра Баттерворта (1), Чебыше­ва (2) и эллиптического (5) от ко­эффициента прямоугольности
Коэффициенты передачи каскадных цифровых НЧ-фильтров Баттерворта и Чебышева

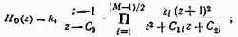
эллиптических

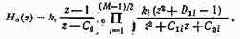
где М — порядок фильтра (при четных М отсутствует сомножитель перед зна­ком произведения); Со, С1i, С2i, Dij — коэффициенты фильтра; k0, k1 — мас­штабирующие коэффициенты.
Анализируя передаточные характеристики фильтров и их исходные данные, можно ограничить число алгоритмов, реализация которых будет рассматри­ваться на последующих этапах. Если допустимы пульсации частотной харак­теристики, то целесообразно в качестве прототипа использовать фильтры Че-бышева или эллиптические. Из-за наличия нулей передаточной функции, не равных единице, ошибки и аппаратурные затраты эллиптических фильтров больше, чем фильтров Чебышева того же порядка.


Преимущества эллиптичес­ ких цифровых фильтров по сравнению с фильтрами Чебышева того же поряд­ка становятся очевидными при коэффициенте прямоугольности а<1,4 за счет меньшего порядка фильтра.
Таким образом, результатом анализа алгоритмов обработки являются ос­новные параметры их реализации: размерность и число входных подмассивов, порядок фильтра, частота дискретизации, уровень боковых лепестков, время обработки и др.
Моделирование алгоритмов. Для выбора наиболее эффектив­ного конструктивного варианта реализации МПУ необходимо обе­спечить возможность сравнивать различные варианты друг с дру­гом. Различные системы команд и состав МПК БИС затрудняют решение этой задачи. Поэтому для повышения общности пред­ставления алгоритмов и программ применяется их моделирование [43]. Целью такого моделирования является оптимазиция реали­зуемого алгоритма с точки зрения времени его выполнения на различных МПК БИС. Использование графовых моделей позво­ляет также исследовать поток данных МПУ и оценить основные характеристики различных структурных вариантов построения МПУ. С помощью графовых моделей можно анализировать мик­ропрограммы, последовательности команд или алгоритм реше­ния некоторой задачи с учетом возможности подключения аппа­ратных процессоров. Графовые модели алгоритма и программы отличаются только степенью детализации отдельных операторов языка моделирования. ,
Граф программы — это циклический ориентированный граф, вершины X которого представляют различные шаги программы. Вершины связаны друг с другом дугами U, представляющими разветвление и циклы в программе. Граф программы содержит одну начальную вершину х0, предшествующую всем остальным вершинам графа и не имеющую входящих дуг, и одну конечную вершину хк, которая следует за всеми остальными вершинами и не имеет исходящих дуг. Каждой вершине приписывается одно или несколько значений аргументов, которые могут представлять вре­мя выполнения данной вершины, погрешность вычисления, по­требность в памяти для соответствующего шага программы и т.


п. Для определения времени выполнения программы TпР необходима задать, как минимум, tij — время выполнения i-го шага програм­мы j-м МП.
С каждой дугой иij связывается значение вероятности того,. что из вершины Xi управление будет передано в вершину Xj. Если для дуги значение рц не указано, то оно принимается равным единице.
Важной особенностью графовых моделей является их универ­сальность. Они могут успешно применяться для оптимизации мик­ропрограмм. В этом случае каждая вершина представляет собой микрокоманду БИС АУ, а дуги указывают последовательность выполнения этих микрокоманд. Такие модели применимы при проектировании, например, МП БО. Необходимость их обусловле­на тем, что разработка на микрокомандном уровне моделей алго­ритма решения сложных задач, как, например, спектрального анализа, потребует значительного времени и большого объема памяти. В этом случае целесообразно применение блочного мно­гоуровневого моделирования при условии сохранения критериев-на различных уровнях моделирования [44]. Вначале моделирует­ся, например, микропрограмма БО и выбирается оптимальный вариант построения МП БО, затем БО становится сама вершиной-и моделируется уже алгоритм спектрального анализа и т. д.
Графовая модель программы обычно строится на основе ее ло­гической структурной схемы. Построенный граф отображает структуру программы. Затем определяются параметры модели. Некоторая часть этих параметров: размер подмассивов входных данных N, число подмассивов Lп, число этапов вычисления БПФ L, порядок фильтра М, время вычисления базовой операции Tбо, вероятности рij и другие определяются в результате анализа ис­ходных данных реализуемого алгоритма. Другие параметры мо­дели определяются из анализа заданной элементной базы: МПК БИС, их быстродействия, системы микрокоманд и т. п.
В некоторых случаях, когда назначение параметров модели аналитическим путем затруднительно, разрабатывают вначале ра­бочую версию программы на языке, близком (по составу опера­торов, распределению регистров и т.


п.) к языку моделирования. Она позволяет проверить логику работы моделируемой програм­мы. Кроме того, некоторые значения параметров модели, напри­мер рц, можно получить из анализа этой программы.
Для исследования полученной модели программы обычно тре­буется ее упрощение. Для корректного проведения такого упро­щения принимаются следующие гипотезы: времена выполнения и коэффициенты циклов являются либо константами, либо случайными переменными с независимыми стационарными функциями распределения; вероятности рц не зависят от того, сколько раз выполнялась вершина и откуда было передано к ней управление-В процессе упрощения модели несколько вершин, связанных друг с другом, заменяются одной вершиной с эквивалентными пара­метрами времени выполнения, вероятностей перехода между вер­шинами. Некоторые элементарные преобразования графовой мо­дели показаны на рис. 3.4. Параметры fi, ti и б2i представляют­частоту повторения, математическое ожидание и дисперсию вре­мени выполнения вершины Xi. Параметр рij представляет вероят­ность передачи управления из (вершины х, в вершину Xj.
При упрощении графовой модели программы необходимо тща­тельно проверить предположения о независимости времени вы­полнения каждой вершины и вероятности перехода по каждой дуге от параметров других элементов графа. Если существуют вершины, для которых эти предположения неверны, то соответст­вующие части графа не упрощаются. Упрощения графовых моде­лей проводятся формальными методами, например с помощью-подсистемы CSS [43].
Модель программы может быть удобно представлена в таблич­ной форме. Существует много способов представления модели; в простейшем из них граф, содержащий n вершин, представляется таблицей из n строк. Каждая строка состоит из следующих эле­ментов: описания выполняемой операции, временных характерис­тик выполняемой операции для всех исходных МП, указателей-вершин-последователей и значений вероятностей переходов в эти вершины-последователи (табл. 3.3).
В табл. 3.3 дано простейшее описание элементов вершины гра­фа. Описание операции содержит информацию только о выпол­няемой функции (сложение, вычитание, умножение и т. п.) и представляется кодом. В более сложных случаях описание вы­полняемой операции может представлять последовательность опе­раторов языка моделирования или при описании действий для определенной вершины модель может использовать генератор слу­чайной величины с заданным распределением и т. п.
Временные характеристики выполняемой операции в простей­шем случае представляют собой среднее время tij выполнения:

Содержание раздела

---

---