при оптимальном размещении логических элементов
|
N |
102 |
103 |
104 |
105 |
10е |
|
К |
4,31 |
6,32 |
9,28 |
13,62 |
20 |
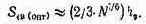
Сокращение линейных размеров соединений и расстояния между ними приводит к росту омического сопротивления проводников и увеличению паразитных реактивностей, влияющих на быстродействие и помехоустойчивость проектируемых БИС. Среди структурных и схемотехнических методов, позволяющих сократить число межэлементных соединений и повысить производительность МПУ, следует отметить: конвейерные структуры; вычисление приращений iK функциям, а не самой функции; использование поразрядной обработки информации; многомикропроцессорные системы с перестраиваемой структурой.
Принципы построения МПУ с использованием приведенных выше методов рассмотрены в ряде работ, например [33, 39].
Таким образом, разработка перспективных методов конструирования связана с решением конструктивно-технологических и схемотехнических задач, обеспечивающих повышение быстродействия и надежности, снижение потребляемой мощности и площади межэлементных соединений МПУ.
Глава 3
автоматизация конструкторского синтеза микропроцессорных устройств и оценка эффективности их применения в рэа
3.1. ВЫБОР КРИТЕРИЯ ОЦЕНКИ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ МИКРОПРОЦЕССОРНЫХ УСТРОЙСТВ
При выборе этого критерия необходимо, в первую очередь, учитывать особенности построения и применения МПУ в составе РЭУ. Проведенный в § 2.2 анализ примеров использования МПУ в РЭА выявил основные особенности: решение задачи в РМВ, распараллеливание выполнения задачи, т. е. использование наряду с МП аппаратных процессоров; наличие возможности перераспределения выполняемых функций между МПУ и РЭУ и разработки для этого специальных интерфейсных схем и периферийных устройств. Кроме того, в данной работе рассматриваются, в основном, специализированные МПУ, конструктивно встраиваемые в РЭА. Конструкция таких МПУ должна иметь минимальную массу и объем, ограниченную потребляемую мощность и высокую надежность.
Задача оценки эффективности применения МПУ в РЭА ставится следующим образом: МПУ должно решать исходный алгоритм в рамках заданных ограничений на его реализацию при минимуме затрат. Затраты на реализацию алгоритма характеризуются рядом скалярных критериев, наиболее важными среди которых являются: масса, объем МПУ, надежность по внезапным отказам, тепловой режим, стоимость.
Оптимизация МПУ по перечисленным конструктивным параметрам (как и любая задача оптимального проектирования) является задачей многокритериальной (векторной) оптимизации.
Для решения задач многокритериальной оптимизации в инженерной практике используется ряд методов, позволяющих векторный критерий свести к скалярному [40]. Каждый метод имеет свои преимущества и недостатки, но все они позволяют довести процесс оптимизации до выбора единственного решения. В задачах конструкторской оптимизации МЭА наиболее часто используется комплексный показатель качества [27]
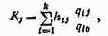
где hij — весовые коэффициенты; qi0 — нормирующий делитель; qij — значение i-го критерия при j-х условиях.
С учетом особенностей применения МПУ в РЭА комплексный показатель качества может быть представлен в следующем виде:
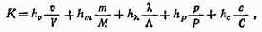
где hv, hm, hi , hP, he — весовые коэффициенты объема, массы, надежности, потребляемой мощности и стоимости МПУ соответственно: v, т, X, р, с, V, М, Л, Р, С — объем, масса, интенсивность отказов, удельная рассеиваемая мощность, стоимость и их нормирующие делители, в качестве которых могут быть взяты одноименные конструктивные параметры всего РЭУ.
Надежность по внезапным отказам является одним из параметров, определяющим условную эффективность всего РЭУ. Для модульных конструкций, предусматривающих возможность перераспределения функций в случае отказов отдельных модулей, интенсивность отказов всего РЭУ определяется из выражения
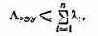
где Лi — интенсивность отказов г-го функционально-конструктивного модуля.
При независимом проектировании отдельных моду лей значение Лi не должно превышать некоторого допустимого-Ядоп, определяемого из условия обеспечения требуемой величины Л РЭу.
Значение удельной рассеиваемой мощности при заданной температуре окружающей среды во многом определяет тепловой режим МПУ, а значит, и перегревы элементов конструкции. Поскольку эти перегревы согласно ТУ имеют допустимые значения, то и удельная рассеиваемая мощность имеет одностороннее ограничение (р<рдоп).
Важным параметром, характеризующим эффективность применения МПУ, является его стоимость. Методика оценки экономической (эффективности применения МПУ приведена в [41]. Используя эту методику, можно определить стоимость разрабатываемого варианта МПУ. Эта стоимость не должна превышать некоторого допустимого значения сДОп, назначаемого с учетом стоимости всего РЭУ, масштаба его выпуска и т. п.
Итак, для случая использования МПУ в РЭА комплексный показатель качества может быть представлен в следующем виде:
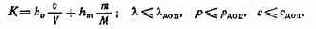
Масса и объем МПУ могут быть определены из следующих выражений:
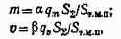
где qm, qv — коэффициенты дезинтеграции массы и объема МПУ; S2 — площадь всех монтажных плат МПУ; а, р, ST.M.n — соответственно масса, объем и площадь типовой монтажной платы, в качестве которой может быть взята монтажная плата, имеющая минимальные размеры из стандартного ряда, кратные размерам всех монтажных плат МПУ.
Подставив значения т и v в (3.2), получим
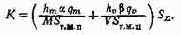
В уравнении (3.3) стоящее в скобках выражение является константой для конкретного случая применения МПУ. Поэтому экстремум K совпадает с экстремумом Sz, т. е. минимизация суммарной площади монтажных плат позволяет минимизировать объем и массу МПУ. С учетом ограничений по надежности, удельной рассеиваемой мощности и стоимости этот критерий может быть использован для оценки эффективности применения МПУ в РЭА.
Необходимо отметить, что 52 не является единственным критерием. В большей степени он отражает специфику применения МПУ в бортовой РЭА. Для других применений МПУ в РЭА критерий может быть иным. Например, при проектировании МПУ, эксплуатируемых в условиях ограниченных энергетических ресурсов, т и v могут стать ограничениями, а оценка эффективности применения будет проводиться по минимуму р и X. Для МПУ, используемых в бытовой РЭА, особое значение приобретает стой? мость с. Если из особенностей конкретного применения МПУ не удается определить целесообразные ограничения конструкторских параметров, то оценка эффективности применения проводится по критерию (3.1). Значения весовых коэффициентов могут быть на значены, например, методом экспертных оценок с учетом особен ностей конкретного применения МПУ.
Итак, оптимальным МПУ будем считать устройство, обеспечивающее решение исходного алгоритма в рамках заданных ограничений и при минимуме суммарной площади монтажных плат Sz:

где б, бдоп — среднее квадратическое значение погрешности вычислений МПУ и его допустимое значение; Тпр, Т — время выполнения программы МПУ и его допустимое значение; L — максимальное число различных вариантов построения МПУ.
Исходными данными решения задачи являются: реализуемый алгоритм (А), ограничения (О) на реализацию А, заданная элементная база реализации (МПК. БИС, ОЗУ, ПЗУ, цифровые микросхемы и др.).
Решение задачи включает ряд этапов.
1. Анализ алгоритма и ограничений на его реализацию. На этом этапе анализируются основные алгоритмы реализации задачи, осуществляется предварительный выбор алгоритма, например по минимуму числа операций умножения. Оценивается возможность реализации алгоритма на имеющейся в распоряжении разработчика элементной базе. Осуществляется оценка необходимости разработки специальных периферийных устройств и др.
2. Генерируются различные конструктивные варианты реализации алгоритма А на заданной элементной базе.
Каждый вариант должен удовлетворять ограничениям (3.4). Для уменьшения размерности задачи она решается методом отсечений. Вначале определяются МП, удовлетворяющие функциональным ограничениям на реализуемый алгоритм, т. е. Тпр<Л и ст<бдоп; МП, не удовлетворяющие этим ограничениям, из дальнейшего рассмотрения исключаются. Генерируются только конструктивные варианты МПУ, соответствующие ограничениям (3.4). Для каждого варианта определяется 52.
3. Наиболее эффективным будет считаться вариант построения МПУ, имеющий минимальное значение 52 .
3.2. АНАЛИЗ И МОДЕЛИРОВАНИЕ АЛГОРИТМОВ
Основной задачей этапа анализа и моделирования алгоритмов является обоснование требований к МПУ. Недостаточно тщательно обоснованные исходные данные приводят к неоправданным ухудшениям его конструктивных и функциональных параметров или к тому, что МПУ не будет в состоянии выполнять возложенные на него функции.
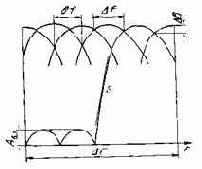
Рис. 3.1. Основные параметры гребенки фильтра слектроанализатора
Проследим процесс анализа алгоритмов на примере распространенных задач цифровой обработку сигналов: спектрального анализа и цифровой фильтрации [2, 30].
Спектральный анализ. Спектроана-лизатор представляет собой гребенку узкополосных фильтров, на вход которой подается сигнал с динамическим диапазоном d, уровнями напряжения UМакс и шума 0ш, диапазоном частот ДF. Выходными параметрами являются требования к гребенке фильтра: точность спектрального анализа, определяемая полосой пропускания фильтра Дf, амплитуда пульсаций и неравномерность частотной характеристики на вершине ДВ, величина внеполосного затухания или уровень боковых лепестков частотной характеристики Лб.л, крутизна ската вне полосы S, расстояние между центральными частотами соседних фильтров 6f (рис. 3.1). Чаще всего гребенка таких фильтров реализуется на основе алгоритма БПФ.
На рис. 2.5 изображена структурная схема вычислителя БПФ, на входе которого включен формирователь квадратур (ФК).
Использование ФК позволяет перенести спектр частот в нулевую область, а применение двух АЦП — в 2 раза снизить частоту дискретизации Fд. Наибольшего внимания требует обоснование допустимых отклонений амплитудной и фазовой характеристик ФК от идеальных. Синфазную и квадратурную составляющие на выходе реального ФК можно представить в виде [2]:
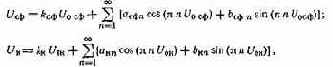
где Uосф, U0K — синфазная и квадратурная составляющие идеального ФК; kсф, kK — средние наклоны амплитудных характеристик; аСф n, а,кп, bсф n, bк n — коэффициенты разложения в ряд Фурье ложного сигнала, возникающего из-за отклонений амплитудных характеристик от идеальных.
Нелинейность амплитудных характеристик разных каналов приводит к появлению на выходе ФК искажений, ложных сигналов. Если принять, что все коэффициенты нелинейности, кроме ЬСф i и &кь равны нулю, а йСф=&к=1, что соответствует случаю, когда нелинейность можно представить отрезкам синусоиды, то выражение (3.5) примет вид
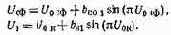
Задаваясь конкретным видом входного сигнала и раскладывая UСф и UH в ряд, можно оценить уровень ложных сигналов, которые образуются на частотах, кратных основной частоте.
