Логические элементы
Дата последнего обновления файла 07.06.2005
Области применения цифровых микросхем.
Цифровые микросхемы первоначально разрабатывались для построения электронно-вычислительных машин, получивших в дальнейшем название компьютеры. То есть первое их предназначение было заменить человека при выполнении рутинной работы. Сейчас, наверное, никто и не вспомнит, что слово калькулятор ещё каких-нибудь шестьдесят лет назад обозначало не маленький карманный прибор, а профессию большого числа людей, которые занимались расчётами по конкретным математическим формулам.
Однако вскоре после начала массового производства цифровых микросхем выяснилось, что они оказались очень удобны для управления какими либо объектами. При этом управляемая схема может обычно находиться в двух состояниях. Например: схема может быть либо включена, либо выключена, светодиод может либо гореть, либо не гореть, соединение в телефонной станции может быть или не быть, радиостанция может находиться в режиме передачи или в режиме приёма. В результате цифровые микросхемы практически полностью вытеснили применявшиеся ещё с девятнадцатого века для управления приборами электромагнитные реле и перфокарты.
При выполнении задачи управления для описания состояния объекта достаточно двух значений: напряжение высокое или низкое (положительное или отрицательное) ток протекает или не протекает. Это позволило избавиться от многих неприятных моментов аналоговых схем. Например, ошибка при прохождении через схему не увеличивается (в отличие от шумов), а в ряде случаев даже может быть скомпенсирована. Сами цифровые схемы при правильном использовании не вносят ошибок. Эти свойства цифровых микросхем привели к бурному развитию цифровой техники.
Приведённые преимущества привели к тому, что в дальнейшем цифровая техника стала использоваться и для решения других задач. Например для формирования высокостабильных колебаний для радиотехнических изделий или для использования в часах. Здесь тоже нет необходимости формировать различные уровни напряжения генерируемого сигнала.
Дата последнего обновления файла 13.07.2005
Логические элементы
Любые цифровые микросхемы строятся на основе простейших логических элементов "НЕ", "ИЛИ", "И".
Простейшим логическим элементом является инвертор, который работает в соответствии с таблицей, приведённой на рисунке 1. Этот логический элемент просто изменяет значение входного сигнала на прямо противоположное значение.
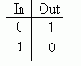
Рисунок 1. Таблица истинности логического инвертора
В качестве инвертора можно использовать обычный транзисторный усилитель с транзистором, включенном по схеме с общим эмиттером или истоком. Схемы, позволяющие реализовать функцию логического инвертирования, приведены на рисунке 2. На рисунке 2а приведена схема инвертора на обычном биполярном транзисторе, выполняющего функцию инвертирования, а на рисунке 2б приведена схема инвертора, выполненного на комплементарных МОП транзисторах.
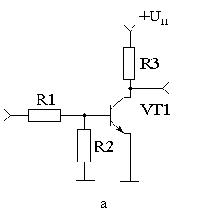
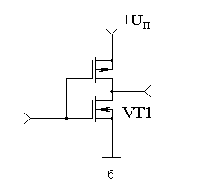
Рисунок 2. Схемы, позволяющие реализовать функцию логического инвертирования.
Как видно из этих схем, функцию инвертирования осуществляет транзистор, включенный по схеме с общим эмиттером (общим истоком). Эти схемы обладают различным временем распространения сигнала и могут работать на различные виды нагрузки. Но независимо от схемы они осуществляют одну и ту же функцию. Для того, чтобы особенности включения транзисторов не затеняли выполняемую функцию, были введены специальные обозначения для цифровых микросхем.
Изображение инвертора на принципиальных схемах не зависит от технологии, по которой изготовлена цифровая микросхема, и приведено на рисунке 2.2. С этого момента схема инвертора в дальнейшем будет приводиться исключительно так, как это показано на рисунке 3.
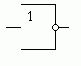
Рисунок 3. Изображение логического инвертора на принципиальных схемах.
Часто
Следующим наиболее распространённым элементом в цифровой технике является элемент, реализующий логическую операцию "И", однако чаще всего существуют не отдельные схемы логического "И", а более сложные схемы, выполняющие одновременно логическую функцию "И" и логическую функцию "НЕ".
Дата последнего обновления файла 30.09.04
Построение произвольной таблицы истинности.
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем "И" "ИЛИ" "НЕ".
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. Для реализации схемы можно воспользоваться как схемами “И” так и схемами “ИЛИ”. В настоящее время наиболее распространены микросхемы, совместимые с ТТЛ технологией, а в этой технологии проще всего получить элементы “И”. Поэтому рассмотрим способ реализации произвольной таблицы истинности основанный на логических элементах “И”.
Для реализации таблицы истинности при помощи логических элементов "И" достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "1" в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую "1", реализуется схемой логического "И" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этой же схемы "И" через инверторы. Объединение сигналов с выходов схем "И", реализующих отдельные строки таблицы истинности, производится при помощи схемы логического “ИЛИ”. Количество входов в схеме “ИЛИ” определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 10:
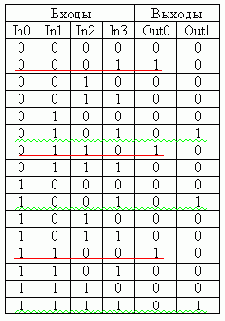
Рисунок 10. Произвольная таблица истинности.
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом.